本文共 1686 字,大约阅读时间需要 5 分钟。
本节书摘来自异步社区《贝叶斯思维:统计建模的Python学习法》一书中的第1章,第1.7节,作者【美】Allen B. Downey,更多章节内容可以访问云栖社区“异步社区”公众号查看
1.7 Monty Hall难题
蒙蒂大厅(Monty Hall problem)难题可能是历史上最有争议的概率问题。问题看似简单,但正确答案如此有悖常理以致很多人不能接受,很多聪明人都难堪于自己搞错了反而据理力争,而且是公开的。
蒙蒂大厅是游戏节目“来做个交易”(Let’s Make a Deal)的主场。蒙蒂大厅难题也是这一节目的常规游戏之一。如果你参加节目,规则是这样的:
- 蒙蒂向你示意三个关闭的大门,然后告诉你每个门后都有一个奖品:一个奖品是一辆车,另外两个是像花生酱和假指甲这样不值钱的奖品。奖品随机配置。
- 游戏的目的是要猜哪个门后有车。如果你猜对了就可以拿走汽车。
- 你先挑选一扇门,我们姑且称之为门A,其他两个称为门B和门C。
- 在打开你选中的门前,为了增加悬念,蒙蒂会先打开B或C中一个没有车的门来增加悬念(如果汽车实际上就是在A门背后,那么蒙蒂打开门B或门C都是安全的,所以他可以随意选择一个)。
- 然后蒙蒂给你一个选择。坚持最初的选择还是换到剩下的未打开的门上。
问题是,你应该“坚持”还是“换”?有没有区别?
大多数人都有强烈的直觉,认为这没有区别。剩下两个门没有打开,车在门A背后的机会是50%。
但是,这是错的。事实上,如果你坚持选择门A,中奖概率只有1/3;而如果换到另外一个门,你的机会将是2/3。
运用贝叶斯定理,我们可以将这个问题分解成几个简单部分,也许这样可以说服自身,“正确”的答案实际上的的确确是对的。
首先,我们应该对数据进行仔细描述。在本例中为D包括两个部分:蒙蒂打开了门B,而且没有车在后面。
接下来,我们定义了三个假设:A,B和C,表示假设车在门A,门B,或门C后面。同样,采用表格法:
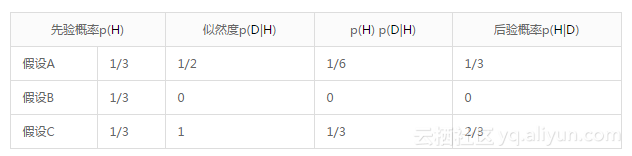
定义似然度需要一些思考,在充分合理的考虑后,我们确信正确的似然度如下:
- 考虑假设A:如果汽车实际上是在门A后,蒙蒂可以安全地打开门B或门C。所以他选择门B的概率为1/2。因为车实际上是在门A后,也就是说车不在门B后的概率是1。
- 考虑假设B:如果汽车实际上是在门B后,蒙蒂不得不打开门C,这样他打开门B的概率就是0(译注:也就是这个假设的似然度为0,不可能发生)。
- 最后考虑假设C:如果车是在门C后,蒙蒂打开门B的概率为1,发现车不在那儿的概率为1(译注:因为在选手已经选了A门这个情况下,可供蒙蒂增加悬念开门的选择只有B和C,而假设C有车,蒙蒂肯定不会选,因此蒙蒂会打开B门的概率为1,也就是在这个假设下,数据D的似然度为1)。
现在我们已经完成有难度的部分了,剩下无非就是算术。第三列的总和为1/2,除以后得到p(A|D) = 1/3,p(C|D) = 2/3,所以你最好是换个选择。
该问题有许多变形。贝叶斯方法的优势之一就是可以推广到这些变形问题的处理上。
例如,设想蒙蒂总是尽可能选择门B,且只有在迫不得已的时候才选门C(比如车在门B后)。在这种情况下,修正后的表如下:
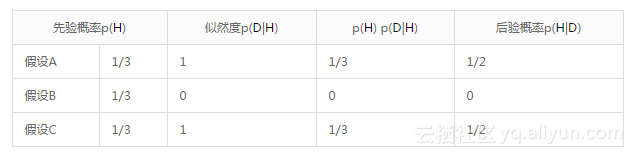
因此,对A和C,似然度是相同的,后验也是相同的:p(A|D) = p(C|D) = 1/2,在这种情况下,蒙特选择B 门显示不了车位置的任何信息,所以无论选手选择坚持不变还是改变都无关紧要。
反过来的情况下,如果蒙蒂打开门C,我们就知道p(B|D) = 1(译注:因为蒙蒂总是优先选择门B,而门D是他打开了门C,因此在假设车在门B后的前提下,他必然会打开门C,概率为1,即p(B|D)=1)。
本章中我介绍了蒙蒂问题,因为我觉得这里有它的趣味性,也因为贝叶斯定理使问题的复杂性更易控制。但这并不算是一个典型的贝叶斯定理应用,所以如果你觉得它令人困惑,没什么好担心的!
转载地址:http://znyil.baihongyu.com/